Advanced Strategies

The following techniques of Advanced Strategies that can be found in SudoKõ are:
1. Single chains
2. Multi-colouring
3. Y-Wing pattern
4. Remote Pairs
5. Unique Rectangles

Single's Chains
Single's Chains, also know as Colouring, Open Chain of Sudoku. There is a very simple chain of clues that works with single candidate numbers only. Players can scan the board for a configuration looking at one number at a time.

Multi-colouring
There are two major types of Multi-colouring and neither is for the faint hearted. Ideally, player needs four coloured pencils and only by scanning the board for single numbers in conjugate pairs. These occur where a candidate exists only twice in any row, column or block. Player can chain these together if there are sufficient numbers of them, just as player did for simple colouring above. In Multi-Colouring player is looking for two or more chains. It is important player does not link up - three or candidates in a cell 'block' a chain link.

Y-Wing

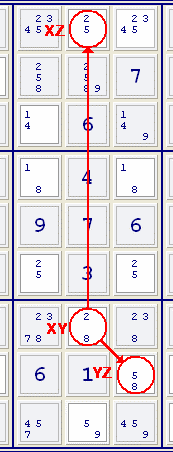Y-Wing also known as XY-Wing is a very advanced technique which can eliminate certain candidates from squares. Given 3 squares where all sqares have exactly 2 candidates, they share the same 3 candidates in the form - xy, yz, xz and one of the squares (the Y 'stem' with canidates xy) shares a group with the other 2 cells (Y 'branches' with candidates xz & yz).

For example, in the diagram, X=2, Y=8 & Z=5. No buddies of both XZ and YZ can contain <5>.

Any squares that are buddies to both XZ & YZ cannot contain Z. It is because it does not matter whether the XY is X or Y, the Z will be in either XZ or YZ, therefore it can be removed from their buddies.

Remote Pairs

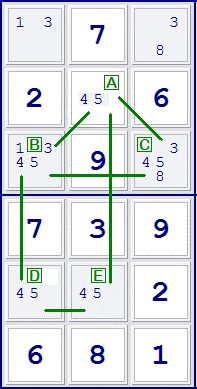Remote Pairs also known as Locked Pair. Pairs occur where two or more squares have the same two possible numbers. A locked pair is two such squares which lock each other in.

For example, in the diagram, the number 4 and 5 occur twice as labelled [A] and [E] as a pair on the same column. The row of [B] and [C] share common number with [A] too as in a block. As the link goes bigger as [A], [B], [C], [D] and [E].

The targets are 4 and 5 which can be got at by an attack from [A], [D] and [E]. The intersection of the ends and no matter which way around number 4 or 5 actually go, either the [B] or [C] can only one of them be a 4 or 5.

Unique Rectangles

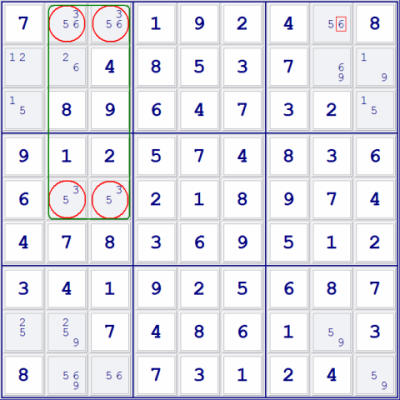Its name comes from a collection of two locked pairs that form a rectangle. Every Sudoku has to have a unique solution; Players are not allowed to create a situation where this rule is violated. It needs to look for four squares that share exactly two blocks, two rows and two columns, if it is a Sudoku with a non-unique solution, and then player could swap the numbers and still have a valid Sudoku with no duplicates. The examples below are a subset of the logic which can be deduced from the requirement of uniqueness, if player comes across a situation which looks similar, and then carefully think about the implications of the Sudoku being left in an invalid state.

There are almost two occurrences of a locked pair in <35>. However, it can never end up with all four squares only containing <35> otherwise it could swap the <3> & <5> and still have a valid solution, which is not allowed. Therefore the <6> in R1 must be in either R1C2 or R1C3 and can therefore be removed from R1C8.