This technique is looking at single numbers in rows and columns. It should be easier to spot in a game as it can concentrate on just one number at a time. The rule is
When there are
- only two possible cells for a value in each of two different rows,
- and these candidates lie also in the same columns,
then all other candidates for this value in the columns can be eliminated.
The reverse is also true for 2 columns with 2 common rows.
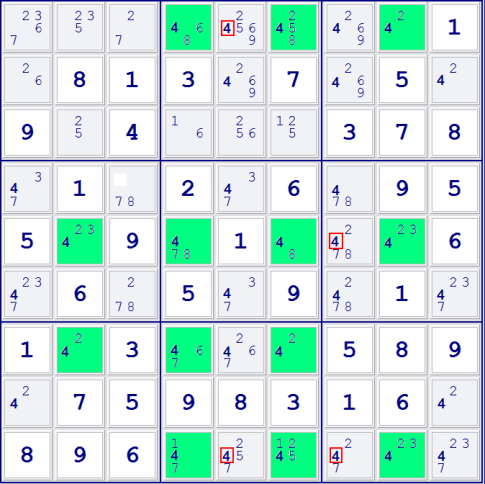
The picture shows a classic x-wing, this example being based on the number six. The X is formed from the diagonal correspondence of squares marked A, B, C and D. The A and B are a locked pair of 6's. So is C and D. They are locked because they are the only 6's in the first and last rows. Therefore that if A turns out to be a 6 then B cannot be a 6, and vice versa. Likewise if C turns out to be a 6 then D cannot be, and vice versa.
What is interesting is the 6's present in the two columns 6 and 9 directly between A and C and B and D. These have been highlighted with yellow boxes. Think about the example this way. A, B, C and D form a rectangle. If A turns out to be a 6 then it rules out a 6 at C as well as B. Because A and CD are 'locked' then D must be a 6 if A is. Or vice versa. So a 6 MUST be present at AD or BC. If this is the case then any other 6's along the edge of our rectangle are redundant.
It can remove the 6's marked in the cyan squares. This is good news because this leaves only a 9 at Z and it can complete.
This strategy works in the other direction as well. If it had two pairs in two columns and those four numbers shared two rows, then it can eliminate any other occurrences of those numbers on the same rows.
With X-Wing it looked at a rectangle formed by four numbers at the corners. This allowed us to exclude other occurrences of that number in either the row or column. It can extend this pattern to nine cells connected by locked pairs. In the example below (concentrating on the number 5) it have three sets of locked pairs at AB, CD and EF. They are all horizontal pairs but they also lock each vertically in a staircase fashion.
The vertical pairing is between AF, BD and CE. Now, in this example it can clearly see that the green horizontal lines connect pairs of 5. Because 5 is also locked vertically the red lines represent columns where if a 5 is not on our grid of nice nodes it can be excluded. There is one such 5 on cell X.
Another way of looking at it is to consider any 5 on the Sword-Fish grid. Pretending for a moment its a real 5 the others in the row and column are repressed. What we're left with is an X-Wing. X-Wing logic then applies to exclude the 5s it can see.
Jellyfish extends Swordfish one further row and column in either:
- four rows such that, in total, four cells are occupied in the row by a candidate number; or
- four columns such that, in total, four cells are occupied in the column by a candidate number
If this configuration is found then it can look in the opposite direction (if by row then down the column, if by column then across the row. If any candidates are found they can be eliminated. After the elimination both conditions above will hold.
By pick any yellow cell in the given example that contains a 4. Keeping an eye on it. Pretend the solution actually is a 4. All others 4s in the row and columns are repressed. The remaining is a Swordfish. The Swordfish logic then applies. Pick any 4 in the Swordfish and it reduces to an X-Wing. Since any combination of 4s on the grid are possible there is no room for 4s outside the grid - that align on the grid rows and columns.